Ancient Insights, Modern Strategy: Sun Tzu, Chanakya, And Nash's Equilibrium

Ancient wisdom offers profound insights into the dynamics of strategic interactions. The renowned Chinese strategist Sun Tzu emphasized this when he stated, "If you know the enemy and know yourself, you need not fear the result of a hundred battles," and "The greatest victory is that which requires no battle." These ideas resonate with Isaac Asimov's assertion that "Violence is the last refuge of the incompetent," highlighting that true mastery lies in achieving one's goals without conflict. Similarly, Chanakya, the ancient Indian philosopher and advisor to Chandragupta Maurya, declared, "A man is great by deeds, not by birth," and cautioned against excessive honesty, noting that "straight trees are cut first, and honest people are taken advantage of first." Together, these teachings underscore the importance of strategy and discernment in navigating complex human relationships.

At the core of these insights lies the concept of strategizing—choosing the most effective course of action in a given situation. Over the past two thousand years, advancements in mathematics, science, and technology have led to the development of various theories of strategic interaction, one of which is game theory. Game theory is a mathematical framework that models socioeconomic interactions among individuals as a game - that is, a function that maps their available strategies to a set of outcomes or stakes, each of which holds different preferences for the players involved. For instance, imagine you discover a magical dollar that will disappear unless shared with someone else. Both you and the other person have competing preferences, each wanting the majority of the dollar for yourselves. This whimsical scenario highlights the core dynamics of economic activity that game theory examines, with the concept of Nash equilibrium at the center of such analyses.

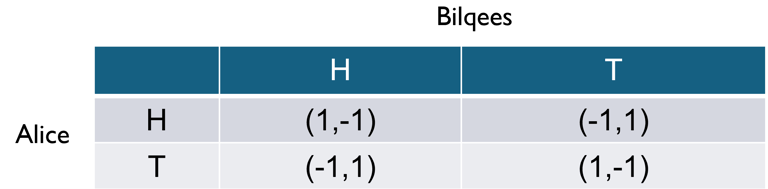
Nash equilibrium refers to a collection of strategies, one per player, where each player responds optimally to the strategic moves of their opponents. In other words, at Nash equilibrium, no player has an incentive to unilaterally change their strategy, as doing so would not lead to a better outcome for them. This notion was proposed by John Nash. While many games have Nash equilibrium outcomes, some do not. Take, for example, the penny-matching game played between Alice and Bilqees. In this game, both players simultaneously choose to reveal either heads (H) or tails (T). The payoff rules are as follows: if both players choose the same side (either H or T), Bilqees loses a dollar and Alice gains a dollar. Conversely, if their choices differ, Alice loses a dollar while Bilqees gains one. This dynamic is captured in the game table below, where the first number represents Alice's payoff and the second number represents Bilqees's payoff.

To find the Nash equilibrium, let's begin by examining the strategy profile (H, H), where both players choose heads. Is H the best response for Bilqees given Alice's choice of H? No, Bilqees would achieve a better outcome by switching to T, as that would allow her to gain a dollar instead of losing one. Therefore, (H, H) is not a Nash equilibrium. Applying similar reasoning to the other strategy profiles, we can conclude that none of them represent a Nash equilibrium in this game.

John Nash was awarded the Nobel Prize in Economics for his groundbreaking work on Nash equilibrium. But if a Nash equilibrium doesn't exist in all games, why the recognition? Nash's key insight was that if players randomize their strategies (for instance, in a penny-matching game, instead of simply choosing heads or tails, they could flip the coins first), an equilibrium is guaranteed to exist in any game with a finite number of players. To demonstrate this, Nash used the Kakutani fixed-point theorem, a mathematical tool that proves certain functions have fixed points—values that remain unchanged by the function. By expanding the scope of the game function to include probabilistic strategies, Nash proved that an equilibrium always exists, appearing as a fixed point in this broader context. Nash's result is profound: it explains why people have relied on coin tosses or drawing straws to fairly resolve conflicts since time immemorial. And all of this in exactly five paragraphs! See his original publication here.

How does one identify Nash equilibrium in probabilistic or mixed strategies? The key principle is to mix strategies in such a way that each player makes their opponent indifferent between their available strategic options. In the penny-matching game, for example, if Bilqees plays heads (H) and tails (T) each half the time, she will make Alice indifferent between responding with heads or tails. Similarly, if Alice also plays heads and tails with equal probability, she will make Bilqees indifferent between her two options. In this scenario, the expected payoffs for both players would be equal to zero. Thus, at Nash equilibrium, both players receive a payoff of zero, which represents a significant improvement over the absence of equilibrium.

Applications of game theory and Nash equilibium extend far beyond economics; they are employed in various fields, including traffic control, computer science, biology, and cybersecurity, underscoring their versatility in understanding strategic interactions across diverse domains. For instance, the penny-matching game can be applied to a soccer match, where the kicker randomizes between kicking the ball to the left or right, while the goalkeeper randomizes between diving left or right. On average, both the kicker and the goalkeeper succeed and fail approximately half the time. Another application is price matching, where two stores compete for customers by attempting to match each other's prices and on average secure a payout of 0, which is always better than a perpetual price war.

There are many fascinating applications of game theory and Nash equilibrium, along with exciting new developments that extend the field into the quantum realm. These topics will be discussed in upcoming posts. Stay tuned!