Beyond Classical Mediation: Enter The Quantum Referee

Depending on the structure of the game—specifically, the payoffs to the players—communication between the players mediated by a referee can correlate players' strategic choices and can lead to Nash equilibria with higher payoffs than those available without such communications. As we discussed in the previous post, Chicken is one such game, where a referee can guide players toward a Nash equilibrium outcome that is better than what can be realized by the players themselves. In contrast, players in Prisoner's Dilemma do not benefit from a referee's mediation, as one strategy (defect) dominates the other (cooperate), making any coordination between the players moves ineffective.

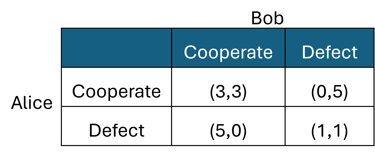
Let's recall the game Prisoner's Dilemma:

Since defecting yields a payoff of 5 or 1 for each player, it consistently offers a better outcome than cooperating, which provides payoffs of only 3 or 0. Even if a referee introduces a probability distribution over the possible outcomes, the expected payoff from defecting—calculated as a weighted average of 5 and 1—remains higher than that of cooperating, which averages over 3 and 0. As defecting always includes a positive payoff, the expected outcome is consistently better, making defection the dominant strategy. Thus, both players will reject any recommendation from the referee to cooperate.

This brings up an interesting question: could the nature of the referee make a difference? If we consider the referee as simply a physical mechanism that correlates players' actions, what if that mechanism was now quantum physical? Could a "quantum referee" introduce new Nash equilibria that provide better payoffs? And might it be possible to resolve the dilemma of the Prisoner's Dilemma if the players engaged via a quantum computer? The answer is yes!

Let's skip the technical intricacies of quantum computing for now and focus on the role it could play in a scenario like the Prisoner’s Dilemma—or, more broadly, what it can fundamentally offer. At its core, a quantum computer has the power to create higher-order correlations and randomization. It achieves these through principles like quantum superposition and entanglement, the Born rule, and the Heisenberg uncertainty principle. For more background, see my previous posts, Quantum Entanglement and the Art of Hotel Breakfast Management and Beyond Al-Kindi: True Randomness from Quantum Sources. In the Prisoner's Dilemma context, the key expectation is clear: a quantum computer would correlate the actions of players Alice and Bob in a way that enables Nash equilibria with better payoffs to emerge.

To achieve these novel and more profitable Nash equilibria, we need to equip Alice and Bob with a quantum computer that mediates communication between them. This requires quantizing the game by encoding the players’ pure strategies and the game outcomes into quantum informational states. This can be done by first imagining that in the classical game, Alice and Bob use coins (without flipping them!) to signal their pure strategic choices: heads for Cooperate and tails for Defect. Now, instead of coins, we give each player a quantum coin, or qubit, whose observable states represent the players' pure strategies. Additionally, each player can manipulate these qubits, placing them in quantum superpositions. These manipulations are done using quantum logic gates, and serve as the players' "quantum strategies," similar to how probability distributions represent mixed strategies. The outcomes of the game then correspond to the observable states of the two qubits. With this encoding in place, we are ready to explore the quantum-enhanced equilibria.

The quantum computer begins by creating maximum entanglement between Alice's and Bob's qubits, establishing a state known as the GHZ state, and informing them of this entangled setup. Next:

1. The quantum referee advises each player on which quantum strategy to adopt. Both Alice and Bob then implement their respective quantum strategies, whether or not they agree with the advice.

2. The referee then disentangles the qubits, creating a quantum superposition that spans all possible game outcomes.

3. A measurement of this quantum superposition yields a probability distribution over the game’s outcomes, representing the final state and payoffs of the game.

This quantum protocol thus enables a quantum correlation between Alice’s and Bob’s choices, with the distribution of outcomes dependent on the entanglement level and the quantum strategies executed.

The analysis now proceeds similarly to the classical case with a referee. In the classical setup, Alice and Bob always end up disagreeing, regardless of the probability distribution the referee uses to correlate their actions. However, in the quantum case, the players consistently agree with the quantum referee when the distribution (1,0,0,0) is used. This distribution aligns both players to cooperate whenever the quantum referee signals them to do so, yielding a payoff of 3 for each. The remarkable aspect here is that, with a quantum referee, it becomes counterproductive for the players to deviate and choose Defect. Despite Defect being the dominant strategy in the classical Prisoner’s Dilemma, the quantum setting shifts the incentives: disagreement with the quantum referee results in a lower payoff, making cooperation the rational choice for both players.

The quantization protocol for the quantum referee described above was originally proposed by Eisert, Wilkens, and Lewenstein in their paper, and is therefore known as the EWL game quantization protocol. This protocol has since been extended to accommodate n-player games, as demonstrated by Du et al. in a subsequent work. With the emergence of early quantum computers, the practical applications of quantized games have gained attention. For instance, in the context of trading strategies, one could represent "going long" (buy first, sell later) as Cooperate and "going short" (sell first, buy later) as Defect within a Prisoner's Dilemma framework, providing a quantum game-theoretic perspective on market sentiment. My main research work and ongoing collaborations are looking into the potential role of quantum games in finance, with a particular emphasis on trading strategies. The preliminary results are promising and offer intriguing insights from multiple perspectives. Although the findings are going to be technical, I’m excited to share them once they’re fully compiled. Stay tuned!