Quantum Information, Game Theory, and the Future of Rationality
Quantum Strategies In Adversarial AI
Adversarial AI has become a focal point in machine learning, especially in the realms of Generative Adversarial Networks (GANs) and misinformation detection. At the core of this field lies a game-theoretic interaction between an AI agent that generates deceptive outputs and another that seeks to classify them accurately. In other settings, one AI agent tries to trick its opponent's classification ability by intermixing real and fake data. The simplest form of this latter scenario can be captured by the zero-sum game called Matching Pennies, demonstrating how deception and classification (detection) evolve toward a mixed-strategy Nash equilibrium. However, the advent of quantum computing has the potential to disrupt this balance, providing one agent the decisive advantage in the form of quantum strategies.
Faisal Shah Khan, Phd
2/21/20254 min read
Matching Pennies is a two-player, two-strategy, zero-sum game in which one player aims to match the opponent’s choice, while the other attempts to do the opposite. The game's name originates from the players’ options—each selecting one side of a coin, Heads (H) or Tails (T), and revealing it simultaneously, followed by payoffs to the players depending on the result.
When abstracted in the context of AI deception and detection:
The Deceiver, an AI agent, selects either real data (R) or fake data (F) for broadcast.
The Detector, another AI agent, attempts to classify the broadcasted data as either real (R) or fake (F).
If the Detector correctly classifies the data, it wins and receives a payoff of +1, while the Deceiver incurs a penalty of -1.
If the Detector misclassifies the data, the Deceiver wins with a payoff of +1, and the Detector is penalized with -1.
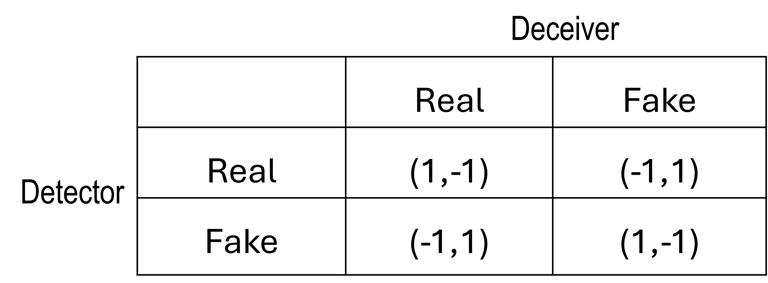
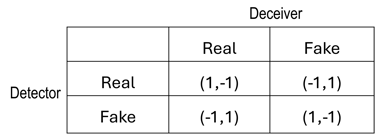
In this formulation, choosing R aligns with showing Heads, while selecting F corresponds to Tails. The resulting dynamics are further illustrated in the payoff table of Figure 1 in which the first number is the payoff to the Detector and the second is the payoff to the Deceiver. Although this setup is conceptually simple, introducing quantum computing into the model can offer novel insights into both game theory and artificial intelligence, leading to studying more complex models.
In the Matching Pennies game, no strategy of either player is a best reply to any of the opponent's strategies, leading to the absence of a Nash equilibrium in "pure" strategies. Instead, both players resort to randomizing their pure strategies, resulting in a "mixed" strategy Nash equilibrium. Before forwarding their coins, both agents toss them. If the coins have the right bias (or if they are fair), then neither player can unilaterally improve their expected payoff by deviating from their mixed strategy. At equilibrium, the Detector plays R and F with equal probability, ensuring the Deceiver has no incentive to favor one strategy. Similarly, the Deceiver randomizes between R and F equally, preventing the Detector from gaining an advantage. This 50-50 strategic play results in both players earning an expected payoff of 0. Practically speaking, in the long term, the Detector can only guess as to which of the data broadcast by the Deceiver is fake, while the Deceiver has no reason to broadcast one type of data (real) over another (fake).
Next, if the AI agents randomize their strategic choices by tossing correlated coins, the resulting Nash equilibrium can sometimes improve. Imagine the correlation between the coins as being facilitated by a flexible metal wire connecting the coins of both agents. With the right choice of correlation mechanism, this correlated joint system of coins can enhance the equilibrium payoffs. In the context of this larger game played with correlated coins, the resulting Nash equilibrium is referred to as a correlated equilibrium in the original game.
A higher-paying correlated equilibrium is not achievable in Matching Pennies. If we conceptualize the correlated coin system as a referee, characterized by a non-factorable probability distribution over the game outcomes and advising the agents on their strategic choices, then a correlated equilibrium only becomes a Nash equilibrium when both agents always follow the referee’s advice. However, in Matching Pennies, due to the zero-sum nature of the game, one player always has an incentive to disregard the referee’s advice and select the other strategy. Therefore, the only correlated equilibrium n Matching Pennies is the trivial one, which corresponds to the mixed strategy Nash equilibrium.
However, this balance shifts when the agents employ quantum strategies. Just as pure strategies can be extended to mixed strategies, and mixed strategies to correlated strategies, so too can correlated strategies be extended to quantum strategies. Quantum strategies are quantum mechanical operations that harness higher-order correlations and randomization, potentially yielding superior Nash equilibria or providing one player with a decisive advantage. Both these outcomes are observed when Hawk-Dove games like Prisoner's Dilemma and Chicken employ quantum strategies.
Quantum strategies can be introduced into a game by substituting traditional coins with ’quantum coins,’ or qubits—units of quantum information processed by a quantum computer. These qubits are then “entangled,” the equivalent of connecting them with a wire, but at the quantum physical level. This combination of quantum strategies and entanglement not only facilitates the generation of correlations between the qubits but also enables the creation of higher-order correlations that are unattainable with regular coins. A particular higher-order correlation, resulting from maximal entanglement, exhibits the property that if one participant flips over their qubit, the state of this qubit remains unchanged. More dramatic is the fact that this action causes the corresponding qubit of the other participant to flip over, even though no further physical intervention is made by either player! This phenomenon underscores the non-local interactions characteristic of entangled particles in quantum mechanics.
In the case of Matching Pennies, agents must randomize their quantum strategies to observe novel equilibrium. These mixed quantum strategies require players to "flip" their qubits before forwarding and measuring them. By employing this higher-order randomization, agents reach a Nash equilibrium when each one randomly selects between two specific quantum strategies with equal likelihood. When executed correctly, this approach guarantees the Deceiver a payoff of +1 while imposing a payoff of -1 on the Detector, with latter unable to improve on this equilibrium outcome. Consequently, quantum strategies create a decisive advantage for the Deceiver over the Detector.