Quantum Strategies: Unlocking Quantum Avantage

In my previous post, I discussed how the guidance of a quantum referee can lead to Nash equilibrium in quantum games that surpass the payoffs achievable through a classical referee in classical games. A striking example is the Prisoner's Dilemma, where, unlike in the classical scenario, deviating from the quantum referee's advice becomes counterproductive for both players. As a result, both players align with the referee's guidance, reaching the Nash equilibrium where they cooperate, effectively resolving the dilemma.

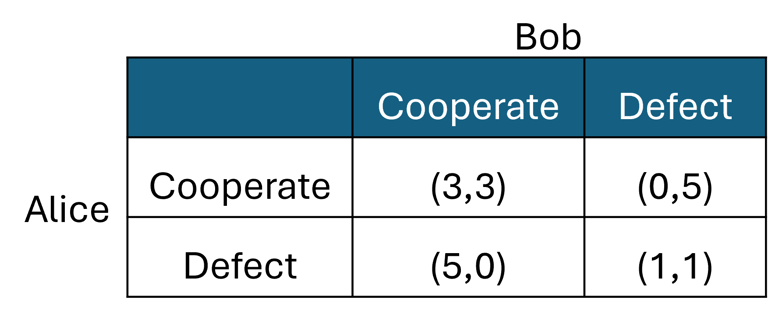
However, an even more dramatic outcome arises when one player is unaware that the game has transitioned to a quantum informational framework. In this scenario, the classical player becomes completely vulnerable, while the quantum player gains a decisive and overwhelming quantum advantage! Recall the Prisoner's Dilemma payoff table:

If Bob is unaware that the game has transitioned to a quantum framework and is under the coordination of a quantum referee, he will disregard the referee's advice to play Cooperate and stick to his original strategy, Defect, as the classical play of Prisoner's Dilemma dictates. To his shock, this decision results in a payoff of zero! In the classical version of the game, Bob was guaranteed a payoff of 1 when following this dominant strategy. However, this guarantee no longer holds in the quantum realm. Instead, the quantum player, Alice, now leverages a decisive quantum advantage.

Another striking example of quantum advantage can be observed in a quantum variation of the penny-flipping game. In the classical version of the game, Alice and Bob take turns flipping a penny or leaving it as is. The penny is placed inside an opaque box, concealing its state from the players until the game concludes. Alice has the first and last moves, giving her two turns, while Bob gets a single turn between Alice's two moves. The objective is simple: if the penny shows heads at the end of the game, Alice wins; otherwise, Bob wins.

If the penny starts in the heads position, the game's dynamics favor Alice in a classical setting. In particular:

• If Bob leaves the penny untouched on his turn and Alice flips it on both her turns, the penny will end in the heads state, securing Alice's victory.

• If Bob flips the penny once on his turn and Alice also flips it once during her two turns, the penny still ends in the heads state, again resulting in a win for Alice.

• Bob can only win if Alice refrains from flipping the penny on both her turns and he flips it once on his turn, leaving the penny in the tails state.

A similar analysis for the case where the game starts with the penny in the tails state reveals that Alice's still enjoys an advantage over Bob. However, the introduction of quantum strategies elevates her advantage to complete and unconditional dominance, allowing her to unilaterally dictate the game's outcome. In this quantum scenario, Bob always loses!

The key to this transformation lies in the use of a quantum penny—a qubit—that can exist in quantum superpositions of heads and tails, manipulated through quantum strategies (quantum logic gates). One particularly powerful quantum superposition that Alice can create is the equal superposition. According to the Born rule, this state has an equal probability of being measured as heads or tails. Crucially, this equal superposition remains unaffected by classical flipping actions. Whether the penny begins as heads or tails, Alice's creation of this superposition renders Bob’s actions—whether flipping the penny or leaving it unchanged—completely ineffective. On her second turn, Alice can apply another quantum strategy to collapse the quantum penny back to the heads state, ensuring her victory every single time.

As long as Bob remains unaware that the game has transitioned into the quantum realm or lacks the capability to counter with his own quantum strategies, he will inevitably find himself at a disadvantage—holding the short end of the proverbial stick in this quantum penny-flipping game. Extending the lessons drawn from these examples of quantum advantage in competitive games, we can envision algorithms themselves as quantum games, much as David Meyer proposed in his groundbreaking work on quantum game theory. In this framework, some components of the algorithms may operate classically, while others leverage quantum principles.

Meyer demonstrates how algorithms can be constructed by extending the quantum penny-flipping game to involve multiple qubits. These algorithms can either exhibit a decisive quantum advantage or lead to Nash equilibrium outcomes, where players achieve the best possible results under specific constraints. Either way, the intersection of quantum game theory and algorithm design remains largely uncharted—terra incognita that beckons for exploration and innovation.