Quantum Information, Game Theory, and the Future of Rationality
The Limits Of Randomization And The Need For Referees
As a kid, I found it amusing that whenever my team won a game—whether it was street cricket, soccer, or something else—the other team would often invoke the “best of three” rule. In other words, they’d suggest playing two more rounds, making the team that wins two games the true victor. It seems that even as kids, we intuitively grasped Nash’s equilibrium theorem involving randomization (see previous post). But is it possible to improve on Nash equilibrium outcomes? Indeed, Nash equilibrium doesn’t always yield the best possible result in a game. A classic example is the Cold War doctrine of Mutually Assured Destruction: while it qualifies as a Nash equilibrium, it was far from the most desirable outcome. Versions of this doctrine still influence global policy today. It turns out that sometimes introducing a referee can help guide players toward outcomes more favorable than those predicted by Nash equilibrium. But why would rational players actually heed a referee’s guidance? The answer to this question was significant enough to earn Robert Aumann a Nobel Prize.
Faisal Shah Khan, PhD
10/28/20245 min read


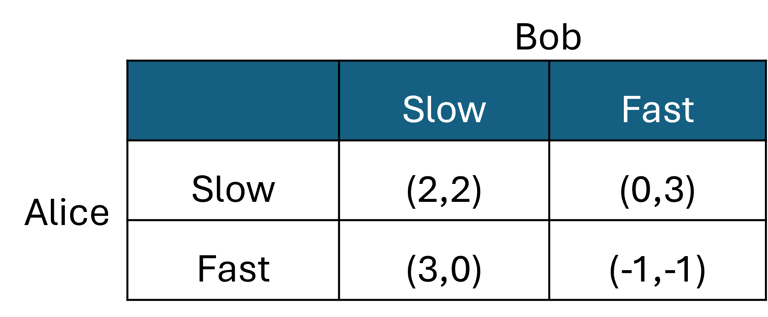
Mixed strategies not only ensure the existence of a Nash equilibrium in games, but they can also offer more favorable outcomes compared to those available in the original pure strategies. An example of this can be seen in the two-player game, Chicken. In Chicken, two players drive toward each other at high speed on a narrow road. Each player has two choices: to continue driving fast or to slow down as they approach the other. To avoid a collision, at least one player must slow down (chicken out). The player who slows down loses face, while the other gains bragging rights. However, if neither slows down, they both face a disastrous crash. This scenario can be modeled with a payoff matrix similar to that used in the penny-matching game of the previous post, as shown below. As usual, the first number represents Alice's payoff from her strategic choice, while the second number represents Bob's payoff from his strategic choice.
This game has two Nash equilibria: one where one player slows down while the other continues at high speed, represented by the strategy profiles (Slow, Speed) and (Speed, Slow). In these equilibria, one player experiences a loss of face. However, a third, more advantageous option exists through mixed strategies where no one loses face. Recall that in a mixed strategy Nash equilibrium, players aim to make their opponents indifferent between their possible responses. In Chicken, both players can achieve this indifference by choosing to go fast half the time and slow the other half. Although both players receive an expected payoff of just 1 in this equilibrium, it is preferable because neither player ends up with a payoff of 0, and the risk of a crash is avoided.
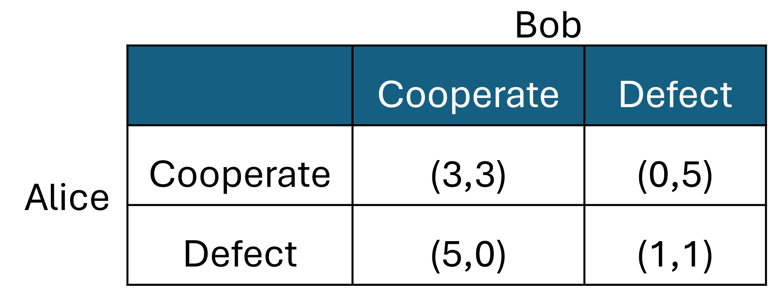
But there are times when randomization does not offer any improvements to a game. This is best exemplified by Prisoner's Dilemma, a strategic scenario involving two individuals (Alice and Bob, again) who make a pact to embezzle money but are caught and sentenced to 10 years in prison. The authorities, unable to find the stolen money, offer both prisoners a deal: if one betrays the other by revealing the money’s location, he will receive a 5-year reduction in his sentence. If neither betrays the other, their sentences remain unchanged.
However, the prisoners know an important legal fact: since their crime was non-violent, if both stay loyal to their pact and refuse to betray each other, the overcrowded prison system will automatically reduce their sentences by 3 years. On the other hand, if both choose to betray and reveal the money’s location, the authorities will only grant them a small reduction—just 1 year each.
Because Alice and Bob cannot communicate with each other in prison, their dilemma is clear: if they trust their partner and stick to the pact, they could both benefit. But if either one betrays the other, the potential reward for cooperation with the partner disappear, and fearing this, both will defect from the pact they made—choosing personal gain over trust. Prisoner's Dilemma can be represented with the following table of payoffs:
The only Nash equilibrium in the Prisoner's Dilemma occurs when both players choose to defect, resulting in a payoff of a 1-year reduction in each player's sentence. Unlike games such as matching pennies and Chicken, the Prisoner's Dilemma has a Nash equilibrium, and it is unique. However, this equilibrium is sub-optimal because both players could achieve higher payoffs by choosing an alternative strategy profile. Specifically, if both players cooperated, they would each receive a better outcome, as deviating from the (Cooperate, Cooperate) strategy makes at least one player worse off. Yet, crucially, (Cooperate, Cooperate) is not a Nash equilibrium.
Could this situation improve if the players used mixed strategies? At first glance, this may seem illogical—after all, a player either cooperates and stays silent, or defects and betrays their partner. How can one "randomize" these binary choices? However, we can imagine the game being played over time and multiple times by different prisoners in the roles of Alice and Bob, and in this broader context, we might ask whether a long-term, average solution emerges in terms of mixed strategies.
However, in the Prisoner's Dilemma, neither Bob nor Alice can reach the level of indifference necessary for a true mixed strategy Nash equilibrium. For both players, defection always provides a higher payoff—either 5 or 1—compared to cooperation, which offers 3 or 0. As a result, they will always choose to defect, even when considering mixed strategies. The mixed strategy equilibrium essentially replicates the original pure strategy outcome, offering no real improvement to the players' situation.
This is where Robert Aumann's Nobel Prize-winning solution comes into play: he introduced the idea of a referee whose advice aligns with the players' preferences. Just as John Nash's groundbreaking work demonstrated how individuals could randomize strategies in situations without clear Nash equilibria, Aumann's insights explain why players would follow a referee's guidance in certain games. Both contributions are profound because they clarify concepts that may seem intuitively obvious but require an exceptional level of intellectual rigor to articulate.
Aumann's referee can enhance the players' outcomes by broadening the range of randomization beyond what players can achieve through simple, independent randomization via mixed strategies. The referee accomplishes this by generating a publicly known probability distribution over the possible outcomes of the game and advising the players to adopt strategies that align with this distribution. Similar to how players use mixed strategies to create indifference among their opponents, the referee aims to correlate the players' behaviors through his guidance. When the players consistently follow the referee's advice for a given probability distribution over the outcomes, the resulting strategy profile is termed a correlated equilibrium. Aumann's paper introducing this idea can be found here (note: the connection to this link is not secure).
The referee's value is especially evident in the game of Chicken. If the referee randomizes the outcomes—(2,2), (3,0), (0,3), and (-1,-1)—using a publicly known probability distribution of (1/3, 1/3, 1/3, 0), where the first three outcomes are equally likely and the fourth never occurs, both Alice and Bob will readily follow the referee's advice, whether it instructs them to slow down or speed up. This is not because they hold the referee in high esteem, but because following his guidance aligns with their best interests. The referee's recommendations improve their outcomes, making it rational for them to comply.
Aumann's work shows us how to design an effective referee, whether in the form of a traffic signal, a negotiator, a legal system, or a judge dispensing justice: the referee's advice must align with the best interests of both players. However, this alignment is not always achievable in every strategic interaction. For instance, in the Prisoner's Dilemma, no advice from the referee can overcome the inherent conflict of interests, leaving the dilemma unresolved. However, quantum computing provides a potential solution to this complex challenge—a topic I'll discuss next time.