Your Data's Quantum Secret: It's All About the Geometry.

In fields like finance, psychology, and artificial intelligence, data sometimes defies classical expectations. Patterns appear that do not quite align with familiar rules of logic or probability. Instead, they resemble behaviors known from quantum physics—like uncertainty, interference, and context-dependent outcomes.

Over the decades, researchers in economics, cognition, and decision science have begun modeling certain human behaviors using mathematical tools from quantum theory—not because the systems themselves are made of quantum particles, but because the models seem to fit better. For instance, when people answer surveys, their responses often depend on the order of the questions—an effect that mirrors the non-commuting nature of quantum measurements. In economic decision-making, the timing of information or offers can lead to context-dependent outcomes—a phenomenon resembling quantum contextuality. These are not just metaphors; in many cases, the quantum formalism genuinely outperforms classical models in predictive power.

This shift has been mirrored in machine learning and data science, leading to “quantum-inspired” methods. These classical algorithms borrow ideas from quantum mechanics to solve difficult problems. They include techniques that embed data into high-dimensional feature spaces—analogous to Hilbert spaces that model quantum mechanics—or that mimic interference patterns to better classify or optimize outcomes. Even though the data is classical, and no apparent quantum physical system is involved in its generation, the structure borrowed from quantum theory appears to improve performance in measurable ways.

But this invites a deeper question. If quantum-inspired models work well even when applied to classical systems, is there something inherently quantum-like in the structure of the data itself? Could it be that we are not just modeling systems “as if” they were quantum, but that some classical data is actually shaped like quantum data—in a geometric (and topological) sense?

The Geometric Connection

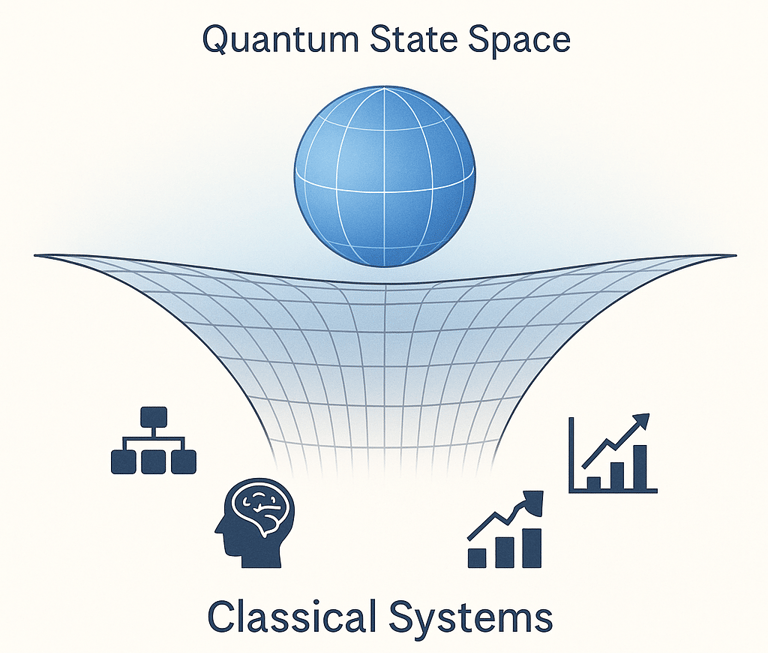
To explore this idea, we can turn to a lesser-known connection between quantum theory and geometry. Quantum states live in complex projective spaces—highly structured, curved manifolds with special symmetries. Crucially, results from differential geometry—especially the Whitney and Nash embedding theorems—tell us that these spaces can be embedded into real Euclidean space, meaning a familiar space of any higher dimension, in a way that preserves their structure. This implies that, in principle, the geometry of quantum state spaces can be realized within classical, real-number-based systems. A well-known example is the Bloch sphere, which represents the state space of a single qubit (what is mathematically known as CP1) as a simple sphere in ordinary three-dimensional space.

These embeddings are more than mathematical curiosities. They suggest that it is possible to encounter classical data—such as that arising in markets, neuroscience, or language—that lies close to, or even on, a submanifold that is the image of an embedded quantum state space. If so, then the quantum-like behavior we observe would not just be a coincidence or the result of clever modeling. It could reflect a deeper geometric reality: that some classical data is structurally quantum, even if it comes from systems we normally think of as non-quantum.

Moreover, if a faithful embedding of the quantum state space exists, we can then—at least in principle—also examine the inverse image of this embedding. This allows us to interpret classical data through its pre-image in the original quantum space, studying it as if it were quantum data. This contrasts with most quantum-inspired approaches, which typically operate on an ad-hoc mapping of classical data into quantum-like representations to extract specific computational advantages, often without preserving the full geometry of the quantum state space.

Modern data analysis gives us tools to investigate this possibility. Techniques from topological data analysis, local dimensionality estimation, and curvature-based manifold learning allow us to detect subtle structure in high-dimensional datasets. If such tools show that a dataset lies on or near the image of a Nash or Whitney embedding of a quantum space, we may have reason to treat it—and model it—differently.

Beyond Conventional Quantum Inspiration

This embedding-based perspective differs fundamentally from typical quantum-inspired computing. While many quantum-inspired methods adapt specific ideas from quantum theory for computational benefit, they often do not preserve its full geometric structure. In contrast, a geometric embedding of quantum state space into classical space allows us to retain the underlying form of quantum processes—even while performing computations on classical hardware. The catch is that these computations are generally inefficient; only true quantum hardware can exploit the full computational speedup. But if our goal is to preserve structure rather than speed, then embedding offers a viable and rigorous path.

All of this leads to a larger, more philosophical implication. Perhaps the distinction between “quantum” and “classical” is not as binary as once thought. If brains, markets, and even language exhibit behaviors better described by quantum mathematics, it suggests that what we call classical systems might sometimes inherit—or approximate—quantum structure. Not in their physical particles, but in the shape and relationships within their data.

In short, maybe classical data does not just act quantum—maybe, in a certain geometric sense, it is quantum. Recognizing this does not require a shift in physics, but a profound shift in how we interpret structure and information. What looks classical may carry shadows of quantum geometry, hiding in plain sight. This brings us back to the value of the geometric embedding approach: it offers a fundamental guarantee that ad-hoc quantum-inspired methods do not. While this theoretical guarantee might not always translate to immediate, practical computational advantages over every heuristic, it provides a crucial conceptual framework. It is the difference between having a precise map of the underlying terrain and merely navigating by trial and error. This rigorous understanding of the data's inherent structure—its quantum geometry—opens the door not just to better models, but to a deeper, more principled understanding of complex systems in the classical world.